La page des polynomes
ax²+bx+c=0
delta = 0
solution(s) : 0
sens de variation :
Objectifs :
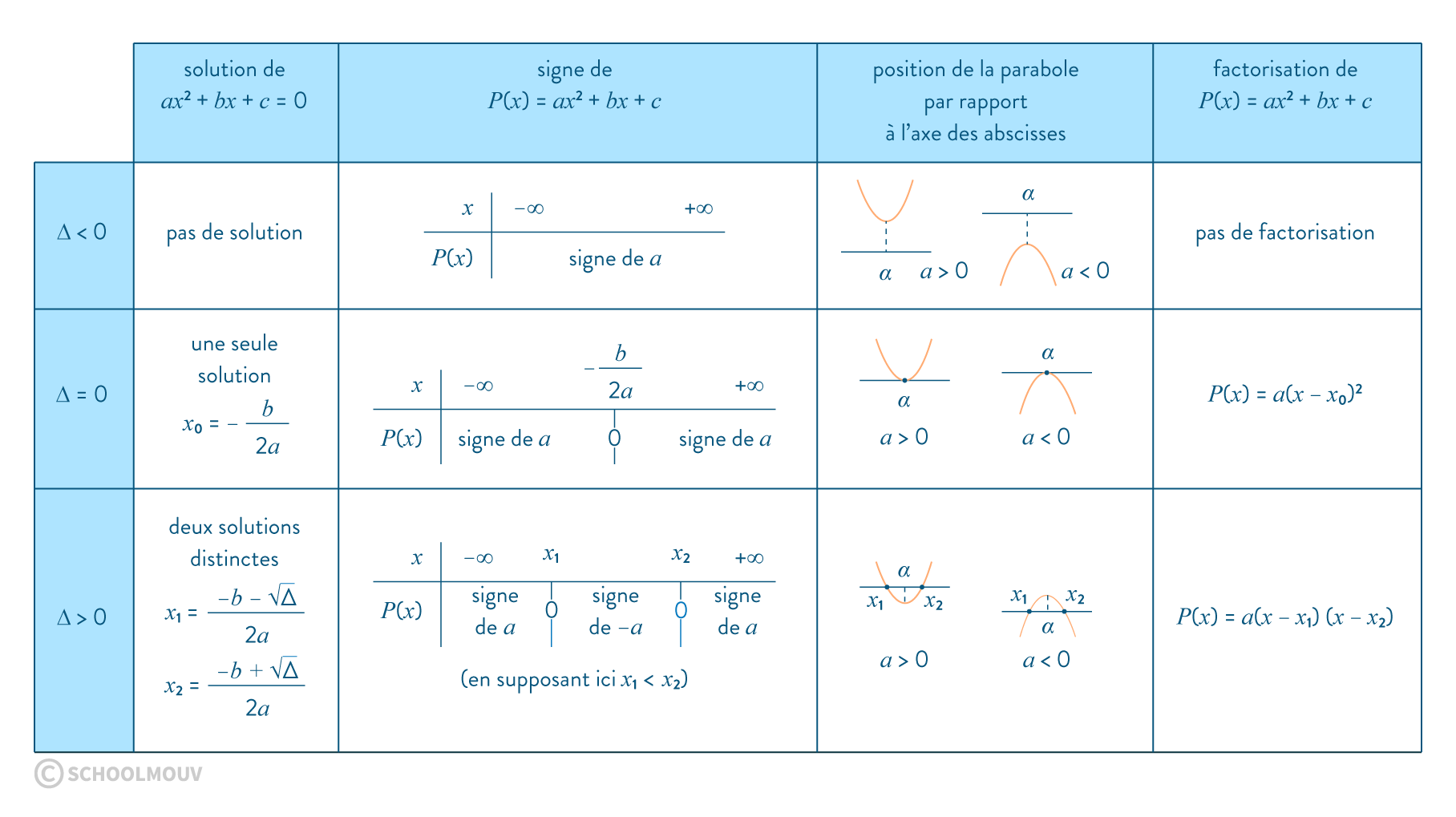
Pour la page sur le chapitre « Polynôme du 2nd degré » le but est de pouvoir calculer le discriminant, rappeler les formules pour résoudre une équation du 2nd degré et faire ces calculs, trouver le sens de variation de la fonction et résoudre des inéquations du 2nd degré.
Carnet de bords :
11/05/2020
 LABLANCHE Maëlle
LABLANCHE Maëlle
J'ai essayé d'intégrer mon programme dans une page web. J'ai rencontré quelques difficultés.
Tout d'abord lorsque j'actualisais la page internet les calculs ne fonctionnaient pas. Avec la console j'ai pu m'apercevoir que Brython n'était pas défini. Je n'avais pas sélectionné le bon répertoire dans lequel il fallait chercher Brython.
Ensuite j'ai eu quelques problèmes d'indentations que j'ai résolu très facilement. Puis il ne trouvait pas la bibliothèque "math" alors j'ai rajouté "" qui permet de pouvoir importer, si nous le souhaitons, les bibliothèques que possède Brython.
J'ai donc pu importer la bibliothèque "math". Je n'ai pas encore terminé d'intégrer mon programme mais il ne me reste pas grand chose à faire.
30/04/2020
 LABLANCHE Maëlle
LABLANCHE Maëlle
J'ai regardé comment utiliser Brython et je me suis entrainée à introduire une phrase en python sur un site html pour comprendre comment Brython fonctionne afin de pouvoir, par la suite, mettre le programme sur les polynômes du second degré sur le site.
Néanmoins Brython est compliqué à utiliser et à comprendre donc pour le moment je n'ai pas bien réussi à "convertir" la phrase.
22/04/2020
 LABLANCHE Maëlle
LABLANCHE Maëlle
J'ai fini de programmer la partie sur les polynômes du second degré et pour ce faire j'ai d'abord importé le module "math" afin d'avoir toutes les fonctions associées à ce module. Ensuite j'ai utilisé des procédures comme print() et des fonctions comme input() qui permet de renvoyer une chaîne de caractères et int() qui va convertir la chaîne de caractères en un nombre entier.
Ensuite j'ai appliqué les formules pour pouvoir calculer le discrimiant (delta), les solutions et donner le sens de variation de la fonction demandée.
Une fonction polynôme du second degré est de forme : ax²+ bx+ c=0
Le discriminant est utilisé pour résoudre les équations du second degré. Grâce à lui nous pouvons calculer les diverses solutions lorsque delta est supérieur ou égal à 0. La formule pour le calculer est b²-4*a*c.
j'ai rentré les différentes possibilités de solution. Lorsque delta est inférieur à 0 la fonction n'a pas de solution. Lorsque delta est égal à 0, la fonction a une solution x0 que nous calculons avec la formule x0= -b/(2*a). Enfin, lorsque delta est supérieur à 0, la fonction a deux solutions x1 et x2 de formule x1= -b-√(delta)/(2*a) et/ x2= -b+√(delta)/(2*a).
Pour le sens de variation j'ai utilisé la propriété suivante : lorsque a est positif les branches sont tournées vers le haut donc la fonction est décroissante sur l'intervalle ]-l'infini ; x0] et croissante sur l'intervalle [x0 ; +l'infini[ (x0 est le minimum atteint par la fonction) et lorsque a est négatif les branches sont tournées vers le bas donc la fonction est croissante sur l'intervalle ]-l'infini ; x0] et décroissante sur l'intervalle [x0 ; +l'infini[. J'ai pris en compte la possibilité d'avoir un a nul, de ce fait il ne resterait plus qu'une fonction du premier degré de type bx+c=0 et le sens de variation est ici déterminé grâce au coefficient directeur b. La fonction est croissante quand b est positif , décroissante quand b est négatif et constante quand b est nul.
Je n'ai pas rencontré de difficultés lors de la programmation.